IBS Magnet - Magnet Dimensions using the Demagnetisation Curve

Unlike other structural elements in mechanics, magnet design is limited by many factors. Here the area and distance between poles in the direction of magnetisation must be determined by the magnetic properties.

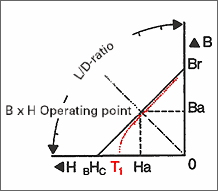
The highest magnetic energy is present if the product of remanence B and coercivity H have reached a maximum. This is the case if the largest possible rectangle forms under the demagnetisation curve of width to height (see figure 1).

The diagram below has a scale on the edge showing the ratio of the length to the diameter (L/D-ratio) of a magnet.

For a disc magnet with 10 mm diameter and 5 mm thickness, the L/D-ratio is 5:10 = 0.5. If a straight line is drawn from 0.5 to zero, the point of intersection on the curve of the corresponding magnet material is the operating point (B x H) of this magnetic material.

If the operating point found is connected horizontally to the width-axis and vertically to the height-axis the remanence and coercivity can now be ascertained.

If width and height have the highest possible value the operating point is in the (B x H) max. value.

For open-circuit magnets used without an iron counterplate or iron poles, the design should always be selected so that the operating point is near to the (B x H) max. value.

If there is an iron counterplate behind the magnet, the magnet length L can be doubled in the L/D ratio for an approximate estimation of the value. This assumes that the thickness of the iron counterplate is sufficient for there to be no magnetic saturation.

If a magnet has square or almost square poles, its pole area can be converted into a circular area by using this formula:

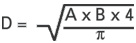
The curves refer to various magnetised materials. They are simplified and do not show the influence of temperatures. A change of temperature causes the operating point to shift on the demagnetisation curve. As long as this occurs within the linear part of the curve all changes of magnetic properties are reversible. This means that after reaching room temperature again the original flux density reappears. Otherwise irreversible changes of the magnetisation are to be expected. Only a new magnetisation brings back the original flux (see red line in figure 1).